编译设计文档

No tag
compiler
Publish Date:   2024-12-01
Word Count:   3.4k

编译设计文档

参考编译器介绍

总体结构

  1. 模块化设计：编译器被划分为多个模块，每个模块负责编译过程中的一个特定任务。例如，有专门处理词法分析的模块（insymbol）、语法分析的模块（block）、代码生成的模块（emit系列函数）等。
  2. 递归下降解析：语法分析部分采用递归下降解析方法，通过一系列的过程（procedure）和函数（function）来识别和构建语法树。
  3. 三地址代码生成：在语法分析的同时进行语义分析和代码生成，生成三地址代码，这是一种中间表示形式，用于后续的优化和目标代码生成。
  4. 错误处理：能够在遇到语法错误时停止编译过程，并报告错误信息。
  5. 内存管理：用于管理符号表、代码存储等。

接口设计

  1. 标准输入输出：通过标准输入输出接口与用户交互，接收源代码文件和输出编译结果或错误信息。
  2. 文件接口：提供了接口来读取源代码文件和输出目标代码文件，以及错误信息和警告信息。
  3. 内部数据结构访问：内部使用了一系列数组和记录来存储符号表、代码等信息，这些数据结构通过一系列的过程和函数接口对外提供访问。
  4. 错误信息输出：提供了errormsg过程来输出错误信息，使得错误处理具有用户友好性。

文件组织

  1. 按照功能模块划分为不同的区块。
  2. 文件开始部分定义了编译器所需的常量和类型，如const和type部分。
  3. 全局变量声明
  4. 主要部分由一系列的过程和函数定义组成，这些是编译器的核心逻辑。
  5. 文件的最后部分是主程序的入口点，从这里开始执行编译器的流程。
  6. 源代码中包含了大量的注释，这些注释有助于理解代码的功能和目的。
  7. 代码按照功能逻辑组织，每个过程和函数都有明确的功能，且通过参数和返回值与其他模块交互。

编译器总体设计

我的编译器项目组织如下：

src/
├── backend
│   └── mips
│       ├── data
│       └── text
├── frontend
│   ├── error
│   ├── lexer
│   └── parser
├── midend
│   ├── llvm
│   │   ├── global
│   │   ├── instr
│   │   ├── stdioInstr
│   │   └── type
│   └── symbol
└── tree
    ├── decl
    ├── exp
    └── func
  1. frontend：存放和源程序有关的前端部分，包括词法分析、语法分析以及错误输出的管理工具类。
  2. midend: 存放语义分析和中间代码生成部分，语义分析主要进行的是错误处理和符号表生成（symbol文件夹中），中间代码使用的是llvm
  3. backend：存放目标代码生成部分，生成的目标代码为mips，由data和text两部分组成，data中是关于全局变量的定义类，text中是指令类
  4. tree：存放语法树相关的类，每个语法成分对应一个类，根据功能的不同分别放在了三个目录下，主要是便于查找。

词法分析

在Lexer类里解析词法。同时使用Token类（如下）管理每个token，其中在LexType是一个枚举类，枚举了所有token类别。

public class Token extends Node {
    private final LexType type;
    private final String value;
    private final int lineNum;
}

注意对字符串和字符中转义字符的处理，根据文法指导书可知：

  • 转义字符不包含\r，其余都有可能在字符常量和字符串常量中出现
  • printf里的字符串常量中转义字符只会出现\n，但其他地方的字符串常量仍可能出现除\r以外的转义字符;

这里我选择在词法解析时把转义字符按照字面量读入，也就是把一个转义字符保存成两个符号。需要注意字符串常量里读入双引号时，不要错误把它识别成字符串结束地方的双引号了。

语法分析

使用递归下降分析法，具体来说，在Parser类里解析语法：

public class Parser {
    private final ArrayList<Token> tokens;
    private int curTokenIndex;
    private Token curToken;
}

词法分析阶段得到的token列表作为输入，采用递归下降的方式逐一解析token：为每个语法规则编写对应的语法解析方法，对于每个token，识别其属于哪条语法规则的FIRST集合的元素（必要时可能还需判断second），然后递归调用对应方法进行解析，最后得到语法树。

对于左递归的文法，如AddExp → MulExp | AddExp ('+' | '−') MulExp，解析时先假定是MulExp，如果后面还有('+' | '−') ，则为刚才的MulExp上面添一层AddExp。

树的每个结点用Node类表示：

public class Node {
    protected ArrayList<Node> children;
    protected int beginLine;
    protected int endLine;
    protected Symbol symbol; // varDef, constDef, funcDef, funcFParams有意义
}

同时为每个语法成分建一个类，并使其继承Node类，方便后续处理。

语义分析

主要完成生成符号表和错误处理的部分。

符号表

使用Symbol类来管理符号，各属性如下：

public class Symbol {
    protected int tableId;  // 当前单词所在的符号表编号。
    protected final String name;    // 当前单词所对应的字符串。
    protected final BType btype;    // 0 -> int, 1 -> char
    protected final boolean isConst;       // 0 -> const, 1 -> var
    protected Node node; // funcSymbol -> funcDef, varSymbol ->varDef/FuncFParam, arraySymbol -> arrayDef/FuncFParam
    protected Value llvmValue;
}

同时让ArraySymbol、FuncSymbol、VarSymbol继承Symbol，实现各自的特殊处理：

  1. 数组符号需要记录长度
  2. 数组、变量符号需要记录初始值
  3. 函数符号需要记录参数表

SymbolTable管理每张符号表。SymbolManager管理符号表生成，为单例模式，方便在全局各个地方调用。

在Node类实现一个semanticAnalysis的方法，用于做语义分析（/符号表生成），然后在必要的语法树的类里复写该方法。由于要处理作用域，因此我们需要在SymbolManager里设置属性记录必要的信息：

public class SymbolManager {
    private static final SymbolManager instance = new SymbolManager();
    private final ArrayList<SymbolTable> symbolTablesList;
    private final Stack<SymbolTable> stack;
    //表示循环嵌套的层数，主要是为了break、continue语句的错误处理
    private int loop = 0;
    //函数参数需加入函数内部的符号表，需要延缓处理
    private boolean needAddFuncFParams = false;
    private ArrayList<Symbol> paramSymbols;
    private boolean isFunc = false;
    // 用于返回语句的错误处理
    private boolean returnStmt = false;
    private int returnLine = -1;
}

错误处理

我写了一个Error类来管理错误，按照题目的输出要求包含了必要的信息（当然为了方便自己查看和debug，可以多扩展一些信息或者复写toString）。

public class Error {
    private final String type;
    private final int lineNum;
}

此外，我还实现了一个单例模式的ErrorList类，用来记录所有错误。

另外，对于重复命名的错误：

左值表达式 LVal → Ident ['[' Exp ']'] // c

该错误统一移到如下两处处理：

语句 Stmt → LVal '=' Exp ';' // h
|...
语句 ForStmt → LVal '=' Exp // h

代码生成

生成中间代码

在这里重新遍历语法树，生成llvm中间代码和重新生成符号表（symbol不重新构建，但是symbolTable重新构建，构建过程和语义分析的过程类似）。同时，类似SybmbolManager，用了一个单例模式的类IRBuilder管理一些要全局使用的东西以及基本块、指令的插入。

public class IRBuilder {
    private static IRBuilder irBuilder = new IRBuilder();
    private Module module;
    private Function curFunc;
    private BasicBlock curBlock;
    private int loop = 0;
    // 用来保存当前循环里break、continue语句需要跳转到的基本块
    private final Stack<BasicBlock> break2BlkStack = new Stack<>();
    private final Stack<BasicBlock> continue2BlkStack = new Stack<>();
}

根据llvm中“万物皆Value”的特性，我的结构如下：

llvm

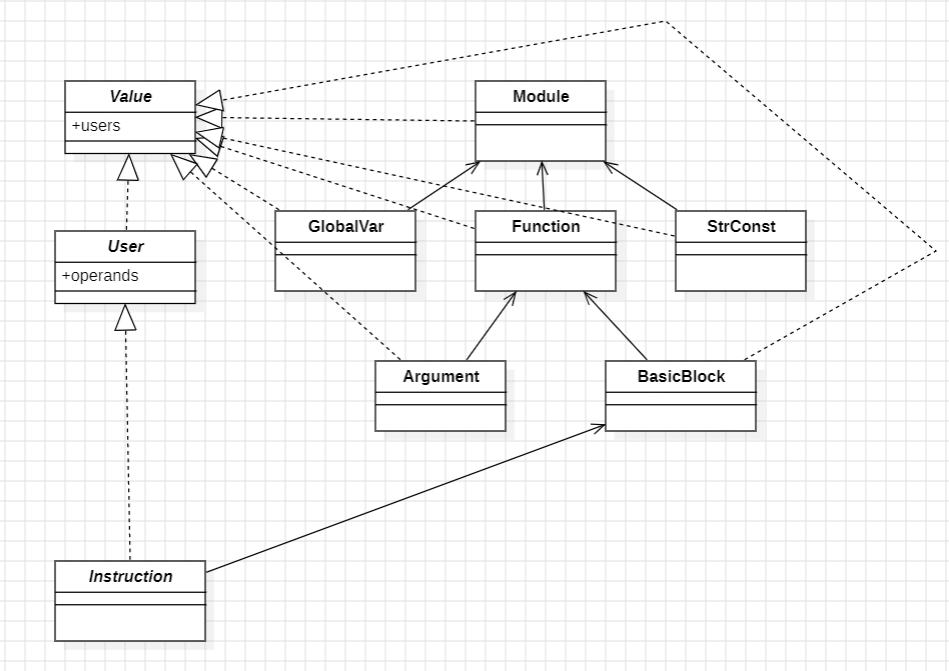
基本按照llvm的官方网站和实验讲座里的实现的，Value、User、Instruction是抽象类，Instruction继承自User（因为它需要记录使用者信息），Instruction下会实现各种指令。其他类都继承自Value。

同时参考官方网站，实现了类型架构，LlvmType会作为Value的属性，相当于它的返回值类型。

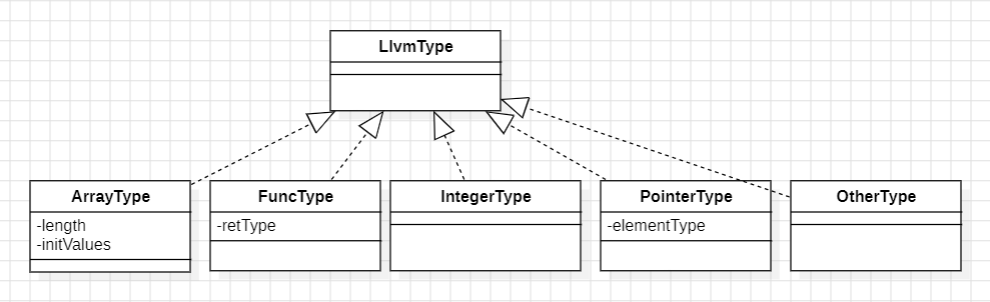
llvmType

在Node类中定义genIR()方法，同时在每个子类中复写该方法，实现具体逻辑。生成中间代码的过程就是递归调用该方法的过程。

需要注意的点：

  1. llvm代码中涉及到三种数据类型i32、i8、i1，不同类型的数据不能直接运算，因此在运算时还需要注意做相互转换，具体细节如下图：

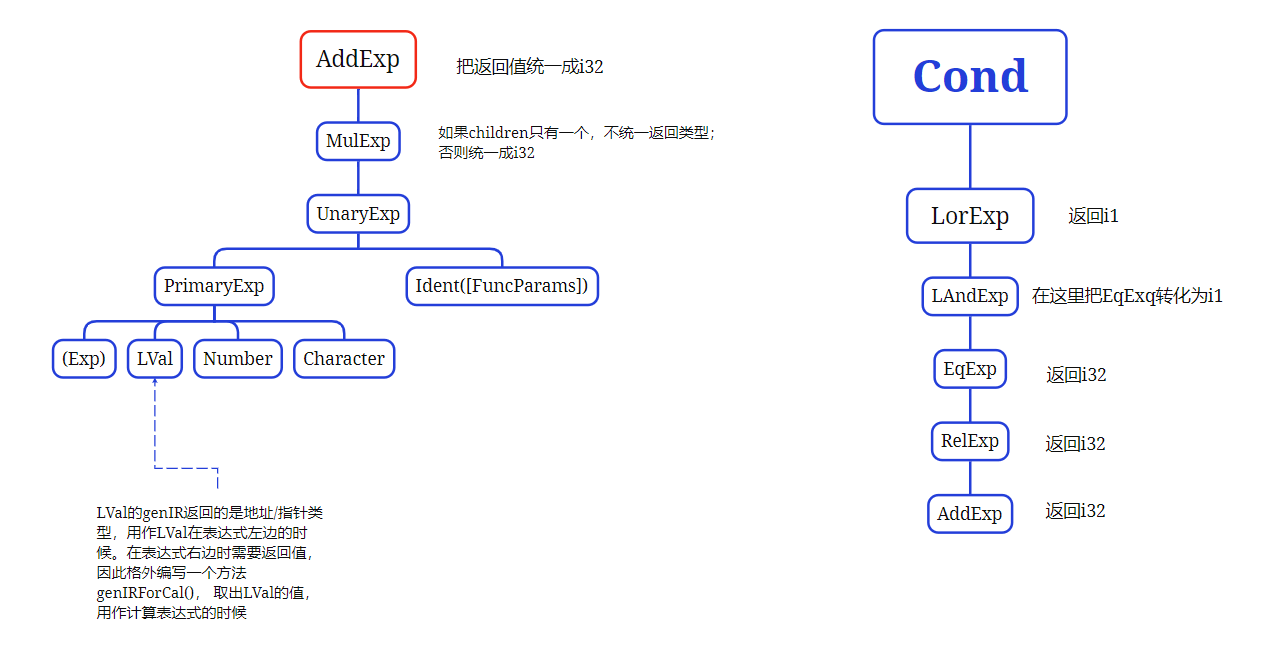
image-20241130143358883

  1. 数组的初始化，教程中提到：

    对于任何有初始值的字符数组，编译器应该在初始化时将未使用的部分置0

    所以数组后面要记得补0，尤其是对于局部数组（debug的血泪教训>_<）。

  2. 对于条件（对应非终结符 Cond）的解析，主要涉及三个基本块：条件为真跳转的目标块，条件为假跳转的目标块，以及条件的运算所属的基本块。这三个块根据表达式的不同（如 if，for）而有一些区别，但是都符合这一模式。在解析前，就准备好这三个基本块，但暂时不将其插入函数中，而到开始解析该基本块时再插入（即把该基本块设置成当前基本块时，IRBuilder.getInst().setCurBlock(trueBlock)。

  3. 对于循环（对应for）的解析，和上述类似，涉及五个基本块，如下图（来源于教程），在我的实现里我把后面四个分别叫做condBlock、loopBlock、stepBlock、endBlock。注意condBlock、stepBlock不一定有。同时让IRBuilder记录endBlock, stepBlock供解析break、continue语句时使用。

for

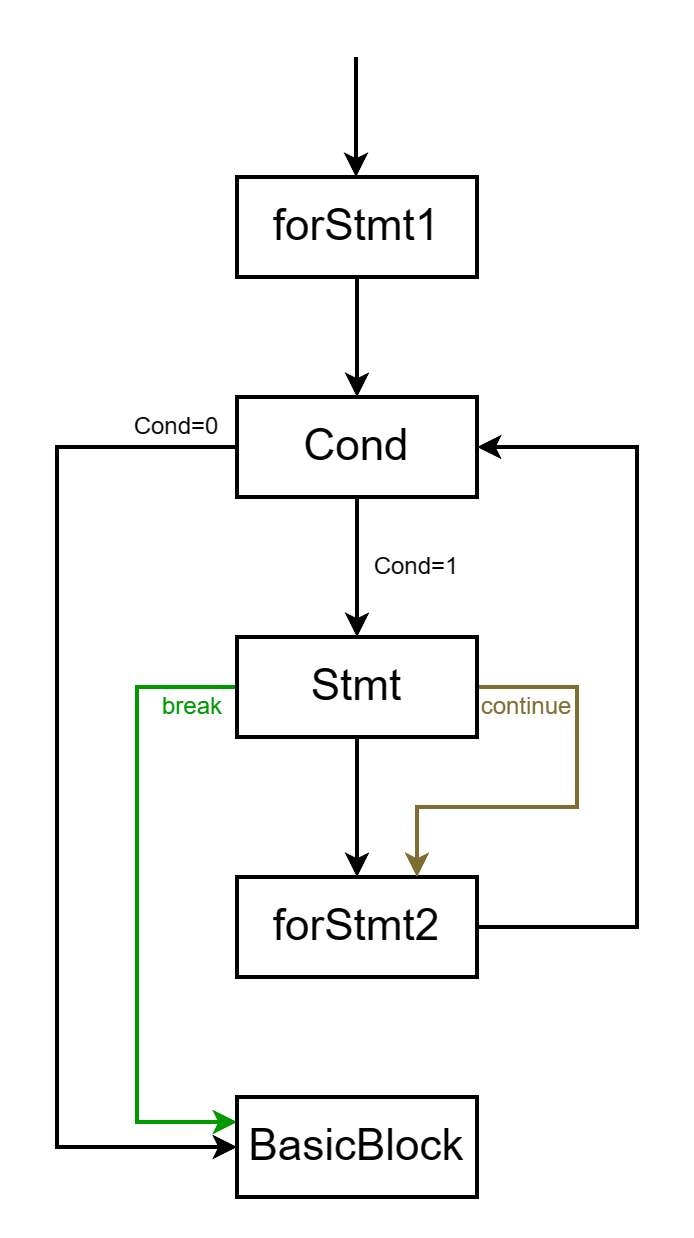
  1. LLVM 中需要对 \n 和 \0 进行转义。

  2. getelementptr指令的格式比较多，我的实现细节如下，这样保证每个a[i]都只需要一条指令就能取到地址。

// 给字符数组赋值，第一个字符赋值用这个
%1 = getelementptr [5 x i32], [5 x i32]* @a, i32 0, i32 3

// 不使用
%2 = getelementptr [5 x i32], [5 x i32]* @a, i32 0 
%3 = getelementptr i32, i32* %2, i32 3 

// 给字符数组赋值，除第一个字符赋值外，其他用这个
// c = s[i]
%3 = getelementptr i32, i32* @a, i32 3
  1. 一个block块只能有一条跳转类型的指令（br/ret），因此需要删除第一条跳转后面的指令

目标代码生成

在llvm中的Value类编写方法genMips，然后在函数、基本块、指令类中复写该方法，实现递归生成目标代码。

一条llvm指令对应一块栈空间或者一个寄存器，其中每条alloca指令一定对应一块栈空间。

Value中的index属性存储Instruction在Function里的序列，与id的不同在于：即使该Instruction没有返回值，其index也有意义；而id用于生成虚拟寄存器（就是%1,%2,…)，没返回值的Instruction的id没有意义。

代码优化

乘法优化

有如下几种情况：

  • 乘以0 rd寄存器直接赋0
  • 乘以1 把rs寄存器move到rd寄存器
  • 乘以2的幂：改为sll语句
  • 其他按普通乘法处理

关键代码：

if (m == 1) {
    if (rd != reg1) {
        new MoveText(rd, reg1);
    }
} else if (m == 0) {
    new LiText(rd, 0);
} else if ((m & (m - 1)) == 0) { // 2的幂
    int k = 0;
    while ((m & (1 << k)) == 0) {
        k++;
    }
    new ALUText(ALUText.Op.SLL, rd, reg1, k);
} else {
    new LiText(reg2, m); // 重新加载operand2
    new MDText(MDText.Op.MULT, reg1, reg2);
    new MFText(MFText.MFType.MFLO, rd);
}

除法优化

不能简单地把2的幂翻译成srl（会有溢出问题），因此我按照讲座里给出的公式来算

image-20241130102745452

关键代码：

if (d == 1) {
    if (rd != reg1) {
        new MoveText(rd, reg1);
    }
} else if ((d & (d - 1)) == 0){ // 2的幂
    // 使用公式：reg1/d= SRA(reg1 + SRL(SRA(reg1, k − 1), 32 − k), k)
    int k = 0;
    while ((d & (1 << k)) == 0) {
        k++;
    }
    new ALUText(ALUText.Op.SRA, reg2, reg1, k - 1);
    new ALUText(ALUText.Op.SRL, reg2, reg2, 32 - k);
    new ALUText(ALUText.Op.ADDU, reg2, reg2, reg1);
    new ALUText(ALUText.Op.SRA, rd, reg2, k);
} else {
    // 处理一般情况 d > 0 且非 2 的幂
    int N = 31; // 假设常量位数为 32 位
    long m = 0;
    int l = 0;
    // 确定 m 和 l
    while (true) {
        l++;
        m = (long) Math.ceil((double) (1L << (N + l)) / d);
        if (m * d <= (1L << (N + l)) + (1L << l)) {
            break; // 满足条件，退出循环
        }
    }
    if (m < (1L << N)) {
        // 使用公式: SRA(MULSH(m, n), l − 1) + SRL(n, 31)
        new LiText(reg2, (int) m);
        new MDText(MDText.Op.MULT, reg1, reg2);
        new MFText(MFText.MFType.MFHI, reg2);

        new ALUText(ALUText.Op.SRA, reg2, reg2, l - 1);
        new ALUText(ALUText.Op.SRL, reg1, reg1, 31);
        new ALUText(ALUText.Op.ADDU, rd, reg2, reg1);
    } else {
        // 使用公式: SRA(n + MULSH(m − 2^32, n), l − 1) + SRL(n, 31)
        m -= (1L << 32);
        new LiText(reg2, (int) m);
        new MDText(MDText.Op.MULT, reg1, reg2);
        new MFText(MFText.MFType.MFHI,reg2);

        new ALUText(ALUText.Op.ADDU, reg2, reg2, reg1);
        new ALUText(ALUText.Op.SRA, reg2, reg2, l - 1);
        new ALUText(ALUText.Op.SRL, reg1, reg1, 31);

        new ALUText(ALUText.Op.ADDU, rd, reg2, reg1);
    }
}

基本块合并

若一个基本块无条件跳转到它的下一个基本块，且下一个基本块只有一个前驱，那么可以直接合并这两个基本块，省去跳转指令。

关键代码：

while (bbIter.hasNext()) {
    BasicBlock curBB = bbIter.next();
    if (prevBB.getInstrs().getLast() instanceof BR br && br.isUncondition() && br.getDest() == curBB
            && curBB.getUsers().size() == 1) { // curBB只有preBB一个前驱
        prevBB.removeInstr(br);
        for (Instruction instr : curBB.getInstrs()) {
            prevBB.addInstr(instr);
            instr.setItsBB(prevBB);
        }
        bbIter.remove();
    } else {
        prevBB = curBB;
    }
}

自己编写的测试程序

  1. str的输出和长度计算

  2. 多于4个参数的函数

  3. 函数调用时实参为常数

  4. 数组初始化时有表达式

  5. 数组某元素作为if中的判断条件

  6. 递归调用的函数

  7. 除法优化

  8. 测试基本块合并优化

Author: CuberSugar
Link: https://slkfoiw.github.io/2024/12/01/compiler/she-ji-wen-dang/
Reprint policy: All articles in this blog are used except for special statements CC BY 4.0 reprint polocy. If reproduced, please indicate source CuberSugar !
No tag
赏
  TOC