改善深层神经网络

深度学习的实践方面

训练集/验证集/测试集(Train/Dev/Test set)

	Train	Dev	Test
小数量	70%		30%
or	60%	20%	20%
百万级数据样本	98%	1%	1%
超过百万	99.5%	0.25%	0.25%
or	99.5%	0.4%	0.1%

偏见与方差(bias&varience)

训练集错误率	1%	15%	15%	0.5%
开发集错误率	11%	16%	30%	1%
	high varience	high bias	high bias & varience	low bias & varience
	过拟合overfitting	欠拟合unfitting	一些地方欠拟合，一些地方过拟合

以上分析基于：human=0% (optimal/base error 理想误差/基误差)

解决办法

graph TD;
    A[high bias]-->B{判断};
    B-->|no|C[high varience];
    B-->|yes|D[bigger network\n train longer\n NN architecture search];
    D-->A;
    C-->|no|E[Done];
    C-->|yes|F[more data\n regularization正则化\n NN architecture search];
    F-->A;

正则化

对较大值的系数进行惩罚

L2 regularization

逻辑回归中：$J\left( {w,b} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {L({\hat{y}^{(i)}},\mathop y\nolimits^{(i)} )} + \frac{\lambda}{2m}|w|^2$ $|w|^2=\sum\limits_{j=1}^{n_x}w_j^2=w^Tw$

神经网络中：$J\left( {w^{[1]},b^{[1]}, …, w^{[l]},b^{[l]}} \right) = \frac{1}{m}\sum\limits_{i = 1}^m {L({\hat{y}^{(i)}},\mathop y\nolimits^{(i)} )} + \frac{\lambda}{2m}|w^{[l]}|^2$ $|w^{[l]}|^2=\sum\limits_{i=1}^{n^{[l-1]}}\sum\limits_{j=1}^{n^{[l]}}{w_{ij}^{[l]}}^2$

用backprop计算dw的值：${\text{w}}^{[l]}: = {\text{w}}^{[l]} - \partial (dw + \frac{\lambda }{m}{w^{[l]}}) = (1 - \frac{\partial \lambda }{m}){w^{[l]}} - \partial dw$

正则化减少过拟合的原因：$\lambda$增大，新的${\text{w}}^{[l]}$减小，隐藏单元的影响减小，存在一个$\lambda$的中间值使得接近”just right”的中间状态

随机失活正则化（Dropout regularization): 设置消除神经网络中节点的概率

在神经网络的训练过程中，随机地丢弃（屏蔽）一部分神经元的输出，即将它们的权重置为零。通过这种方式，可以防止神经网络过度依赖某些特征，从而提高模型的泛化能力和鲁棒性。Dropout技术通常应用于神经网络的隐藏层上，并按照一定的概率p随机失活部分节点，在后向传播时进行相应的参数更新

最常用的实施方法：反向随机失活

e.g.: 以一个三层随即网络为例

1. 定义向量d

   d3=np.random.rand(a3.shape[0], a3.shape[1]) < keep-prob

   keep-prop表示保留某个隐藏单元的概率

归一化输入（normalizing inputs）:可以加速训练方法

将所有图像的像素值缩放到一个特定的范围（通常是 [0, 1] 或 [-1, 1]）

step：

1. 零均值化：${M_j} = \frac{1}{m}\sum\limits_{i = 1}^m {x_j^{(i)}}$ $x_j:=x_j-\mu _j$
2. 归一化方差：${\sigma ^2} = \frac{1}{m}{\sum\limits_{i = 1}^m {({x^{(i)}})} ^2}$ ${x_j}: = \frac{x_j}{\sigma }$

梯度消失和梯度爆炸

梯度爆炸：各层权重w都大于1，层数很大

梯度消失：各层权重w都小于1，层数很大

神经网络的权重初始化

${w^{[l]}} = np.random.randn({n^{[l]}},{n^{[l - 1]}}.*np.sqrt(1/{n^{[l - 1]}}))$

$n^{[l - 1]}$表示第l-1层神经元的数量；如果用的Relu激活函数，sqrt中的1改为2更好

梯度检验：确保backprop正确实施

${\theta _{\text{i}}} = (w_i^{[1]},b_i^{[1]},…,w_i^{[l]},b_i^{[l]})$连接成一个超大向量

$d{\theta _{approx[i]}} = \frac{J({\theta _1},{\theta _2},…,{\theta _i} + \epsilon ,..) - J({\theta _1},{\theta _2},…,{\theta _i} - \epsilon ,..)}{2\epsilon }$验证是否逼近$d{\theta _{[i]}} = \frac{\partial J}{\partial {\theta _i}}$

验证方法：计算两个向量的欧式距离$\frac{||d{\theta _{approx[i]} - d{\theta _{[i]}}||{^2}}}{||d{\theta _{approx[i]}}||{^2} + ||d{\theta _{[i]}}||{^2}}$,$\leqslant {10^{ - 7}}$没问题，$\approx {10^{ - 5}}$可能有问题/bug，$\approx {10^{ - 3}}$有问题

注：

1. 不要在训练中使用grad check，它只用于调试
2. 如果算法的梯度检验失败，要检查所有项，并试着找出bug，注意$\theta$的各项与b、w的各项都是一一对应的
3. 在实施梯度检验时，如果使用正则化，请注意正则项
4. 梯度检验不与dropout同时使用
5. 现实中不会在随机初始化时运行梯度检验

优化算法

Mini-batch梯度下降法

将整个训练样本分成若干份（mini-batch），然后迭代。

假设训练样本m个，分成n份，一次遍历训练集，可以做n次梯度梯度下降

• m<2000时，直接batch gradient descent(就是之前讲的常规梯度下降法)
• m很大时，建议分成$2^n$倍（跟电脑内存存储方式有关）

指数加权平均（Exponentially weighted averages）(统计学中称为指数加权移动平均)

关键公式：${v_t} = \beta {v_{t - 1}} + (1 - \beta ){\theta _t}$

其中$\theta_t$是实际值，整个式子可以看成$v_t$是$\frac{1}{1-\beta}$个数据的平均值

指数加权平均的偏差修正（bias correction）在预估初期，不用$v_t$，而用$\frac{v_t}{1-\beta^t}$

动量梯度下降法（Gradient descent with momentum）

基本想法：计算梯度的指数加权平均数，并利用该梯度更新权值

$$\left\{ \begin{gathered} {v_{dw}} = \beta {v_{dw}} + (1 - \beta )dw \hfill \\ {v_{db}} = \beta {v_{db}} + (1 - \beta )db \hfill \\ \end{gathered} \right.$$ $$\left\{ \begin{gathered} w: = w - \partial {v_{dw}} \hfill \\ b: = b - \partial {v_{db}} \hfill \\ \end{gathered} \right.$$

RMSprop算法（RMS：root mean square均方根，标准差）

$$\left\{ \begin{gathered} {S_{dw}} = \beta {S_{dw}} + (1 - \beta )(dw)^2 \hfill \\ {S_{db}} = \beta {S_{db}} + (1 - \beta )(db)^2 \hfill \\ \end{gathered} \right.$$ $$\left\{ \begin{gathered} w: = w - \partial \frac{dw}{\sqrt {S_{dw}} } \hfill \\ b: = b - \partial \frac{db}{\sqrt {S_{db}} } \hfill \\ \end{gathered} \right.$$

原理：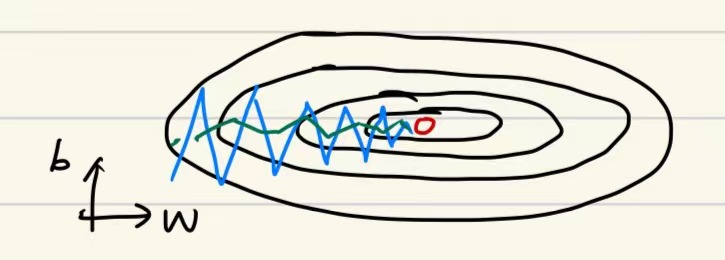

我们希望在横轴（w方向）学习速度快，纵轴（b方向）减缓摆动，所有有了$S_{dw}$,、$S_{db}$，w要除以一个较小的数（$S_{dw}$相对较小），b要除以一个相对较大的数（$S_{db}$较大）。

Adam优化算法（Momentum和RMSprop的结合）

步骤：

1. 初始化：$v_{dw}=0$ $S_{dw}=0$ $v_{db}=0$ $S_{db}=0$

2. 计算Momentum指数加权平均数：

   $$\left\{ \begin{gathered} {v_{dw}} = \beta_1 {v_{dw}} + (1 - \beta_1 )dw \hfill \\ {v_{db}} = \beta_1 {v_{db}} + (1 - \beta_1 )db \hfill \\ \end{gathered} \right.$$

3. 使用RMSprop进行更新

   $$\left\{ \begin{gathered} {S_{dw}} = \beta_2 {S_{dw}} + (1 - \beta_2 )(dw)^2 \hfill \\ {S_{db}} = \beta_2 {S_{db}} + (1 - \beta_2 )(db)^2 \hfill \\ \end{gathered} \right.$$

4. 使用Adam算法，一般要计算偏差修正

   $v_{dw}^{corrected} = \frac{v_{dw}}{1 - \beta _1^t}$

   $v_{db}^{corrected} = \frac{v_{db}}{1 - \beta _1^t}$

   $S_{dw}^{corrected} = \frac{S_{dw}}{1 - \beta _2^t}$

   $S_{db}^{corrected} = \frac{S_{db}}{1 - \beta _2^t}$

5. 更新权重

   $$\left\{ \begin{gathered} w: = w - \partial \frac{v_{dw}^{corrected}}{\sqrt {S_{dw}^{corrected}} + \epsilon } \hfill \\ b: = b - \partial \frac{v_{db}^{corrected}}{\sqrt {S_{db}^{corrected}} + \epsilon } \hfill \\ \end{gathered} \right.$$

学习率衰减（learning rate decay）

加快学习算法的一个办法是随时间慢慢减少学习率

$\partial = \frac{1}{1 + decayrate \cdot epoch - num}{\partial _0}$，epoch-num是训练的代数

$\partial = {0.95^{epoch - num}}{\partial _0}$

$\partial = \frac{k}{\sqrt {epoch - num} }{\partial _0}$

$\partial = \frac{k}{\sqrt t }{\partial _0}$

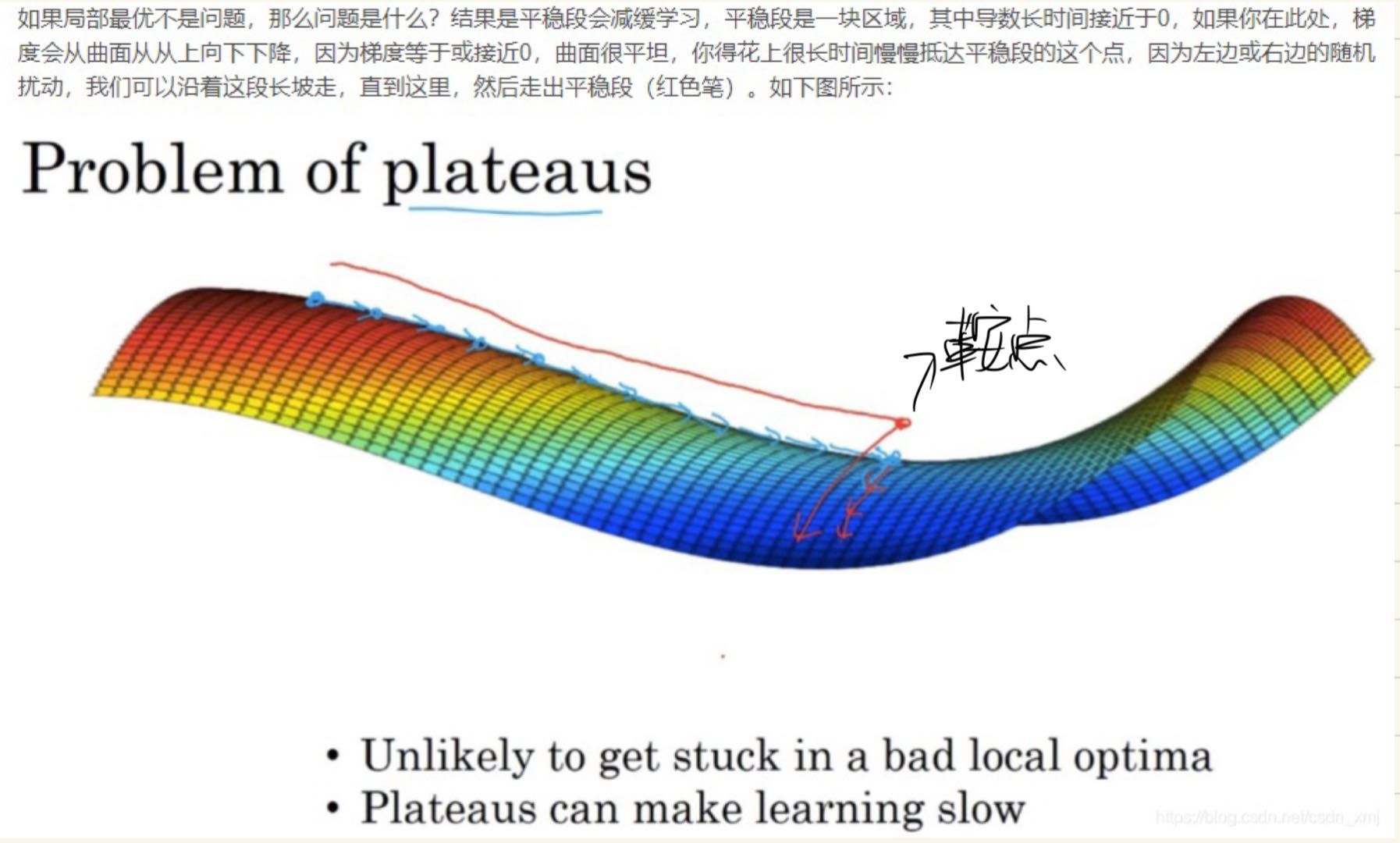
局部最优问题