机器学习导论-个人作业技术报告

选择题目：3 糖尿病诊断

数据集预处理

1. 数据集中存在为布尔值的属性列，先把它们转化成数字（0：False, 1：True)
2. 把标签列提取出来编码，采用标签编码即可（0: NoDiabetes, 1: Prediabetes, 2: Diabetes）

相关代码如下：

def preprocess_data(data):
    # 将布尔值转换为数值
    data = data.replace({True: 1, False: 0}).infer_objects(copy=False)

    # 将 Diabetes 列编码为数值（0: Diabetes, 1: NoDiabetes, 2: Prediabetes）
    le = LabelEncoder()
    data['Diabetes'] = le.fit_transform(data['Diabetes'])

    return data, le

特征选择

数据的样本涉及到特征种类较多，为避免无关特征的影响，我们先对特征进行选择，找出与标签（即糖尿病的情况）相关性最高的几个特征。然后将特征进行标准化，让不同特征的数值范围一致，这样可以让模型更好地进行训练和收敛。

相关代码在model_search.py文件中:

# 特征选择
def feature_selection(data, top_k=9):
    X = data.iloc[:, 1:-1]  # 特征变量
    Y = data.iloc[:, -1]  # 目标变量

    select_top_k = SelectKBest(score_func=chi2, k=top_k)  # 选择排名前k的特征
    fit = select_top_k.fit(X, Y)
    features = fit.transform(X)

    # 提取特征名称
    selected_features_indices = fit.get_support()
    selected_feature_names = X.columns[selected_features_indices].tolist()
    print("选择的特征:", selected_feature_names)
    return features, selected_feature_names

模型探索

该问题是一个分类问题，数据集比较易于处理，考虑从简单的模型开始，如逻辑回归或决策树，逐步过渡到更复杂的模型，如随机森林或支持向量机。这里我选择了如下几种模型：

1. 逻辑回归（Logistic Regression）
2. 高斯朴素贝叶斯（Gaussian Naive Bayes）
3. K近邻分类（K-Nearest Neighbors）
4. 决策树分类（Decision Tree Classifier）
5. 支持向量机（Support Vector Machine, SVM）
6. XGBoost

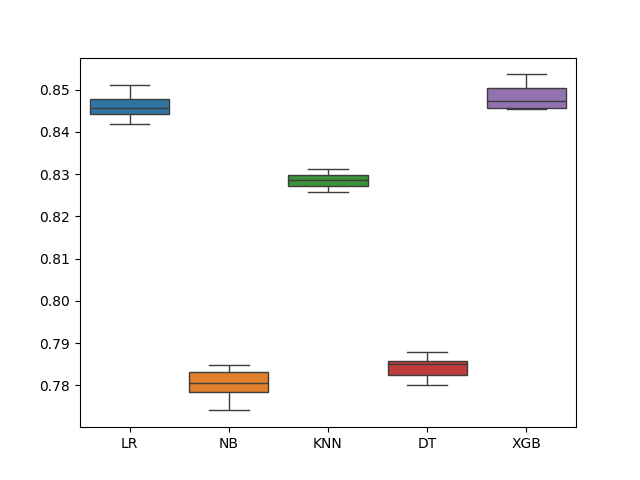
通过交叉检验对每个模型进行评估，以下是各模型在训练集上的交叉验证mP：

SVM耗时较长，后续补充XGBoost模型时没有评估SVM：

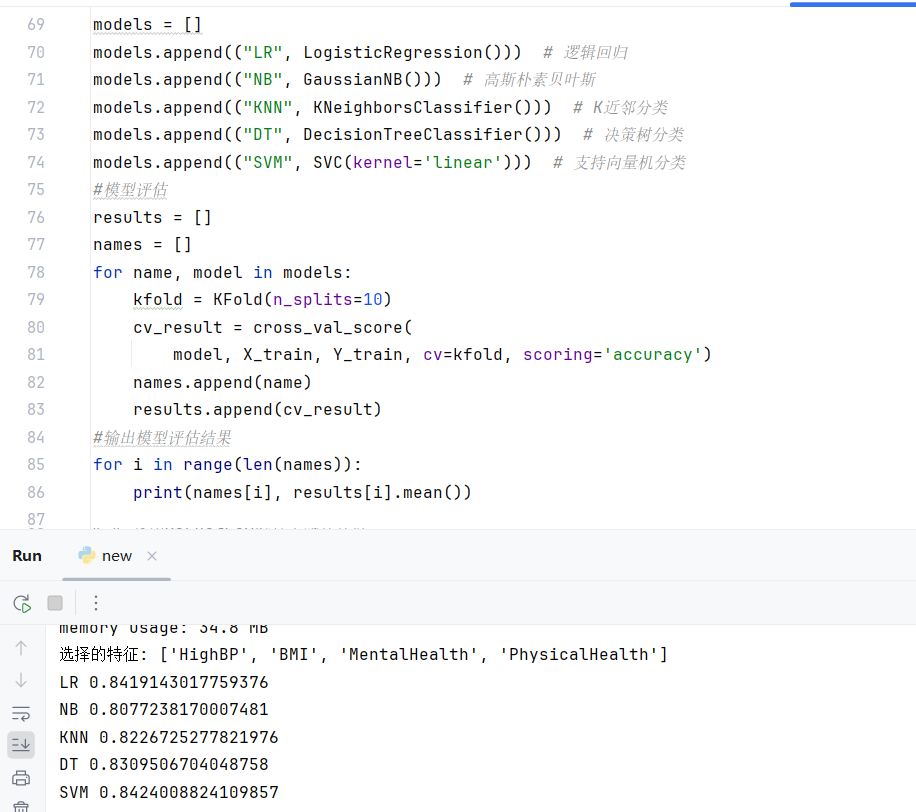
LR 0.8461940174191783
NB 0.7803187407247
KNN 0.8286078911982038
DT 0.7842212562301403
XGB 0.8481994913743092

可以看到逻辑回归、支持向量机、XGBoost的结果较好，因此可以选择这些模型进行接下来的探索。

这部分的关键代码如下：

#模型选择
def model_selection(X_train, Y_train):
    models = []
    models.append(("LR", LogisticRegression()))  # 逻辑回归
    models.append(("NB", GaussianNB()))  # 高斯朴素贝叶斯
    models.append(("KNN", KNeighborsClassifier()))  # K近邻分类
    models.append(("DT", DecisionTreeClassifier()))  # 决策树分类
    models.append(("XGB", XGBClassifier()))  # XGBoost分类
    # models.append(("SVM", SVC(kernel='linear')))  # 支持向量机分类
    #模型评估
    results = []
    names = []
    for name, model in models:
        kfold = KFold(n_splits=10)
        cv_result = cross_val_score(
            model, X_train, Y_train, cv=kfold, scoring='accuracy')
        names.append(name)
        results.append(cv_result)
    #输出模型评估结果
    for i in range(len(names)):
        print(names[i], results[i].mean())

    # 结果可视化
    ax = sns.boxplot(data=results)
    ax.set_xticklabels(names)
    plt.show()

平衡数据集

注意到数据集中NoDiabetes的类别明显比Diabetes和PreDiabetes多，可能导致结果预测不平衡，因此class_weighted选择‘balanced’。这个可以显著提高结果的mP。

另外还采用了SMOTE过采样：

SMOTE 的作用

1. 平衡数据集:
   • 通过生成合成的少数类样本，使数据集中的各个类别的样本数量更加平衡。
   • 这有助于模型更好地学习少数类的特征，提高其预测能力。
2. 减少过拟合:
   • 当数据集不平衡时，模型可能会对多数类进行过度拟合，而对少数类拟合不足。
   • 使用 SMOTE 增加少数类样本可以减少这种偏向，提高模型的泛化能力。
3. 提高模型性能

SMOTE 的工作原理

1. 首先，从少数类中随机选择一个样本。
2. 计算该样本与所有其他少数类样本之间的距离，找到最近的几个样本。
3. 在选择的样本与其最近邻之间随机选择一个点，并生成一个新的合成样本。这个新样本是通过线性插值在两个样本之间的某一位置生成的。
4. 重复上述过程，直到少数类的样本数量达到指定的平衡比例。

相关代码如下：

# 过采样
from imblearn.over_sampling import SMOTE

# 应用 SMOTE 进行过采样
smote = SMOTE()
X_train_resampled, Y_train_resampled = smote.fit_resample(X_train, Y_train)

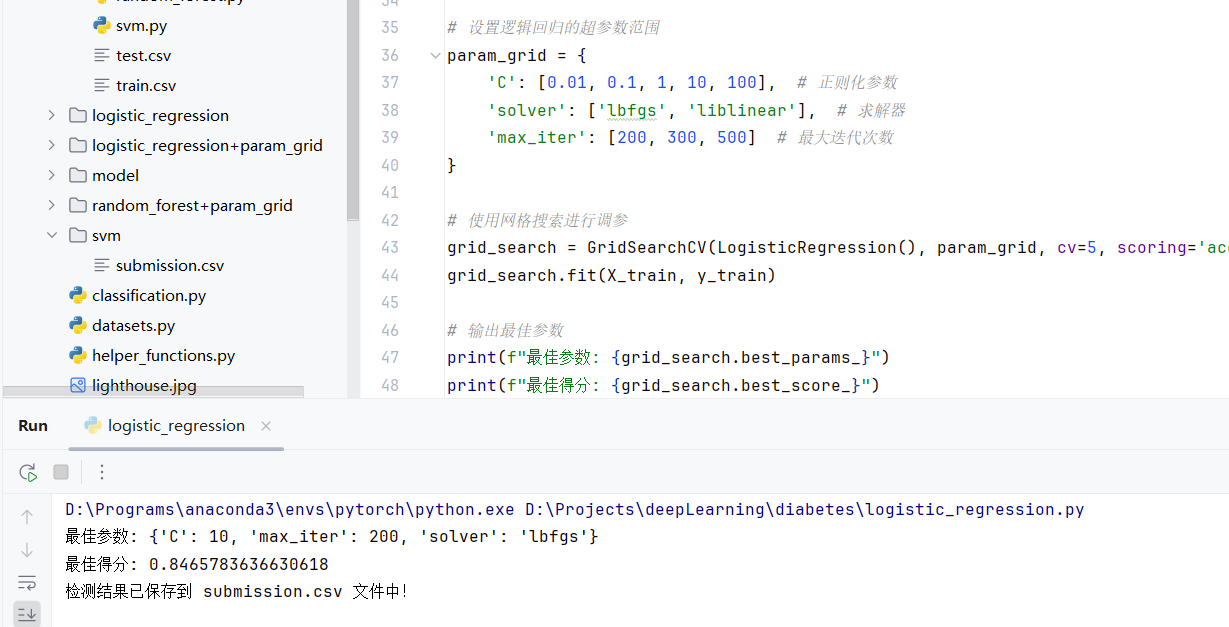
调参

使用网格搜索对参数进行调优，关键代码如下：

from sklearn.linear_model import LogisticRegression
# 使用网格搜索进行调参，并设置 class_weight

# 设置逻辑回归的超参数范围
param_grid = {
    'C': [0.005, 0.01, 0.1, 1],  # 正则化参数
    'solver': ['lbfgs', 'liblinear'],  # 求解器
    'max_iter': [100, 150, 200]  # 最大迭代次数
}

from sklearn.model_selection import GridSearchCV

grid_search = GridSearchCV(LogisticRegression(class_weight='balanced'), param_grid, cv=5, scoring='accuracy')
grid_search.fit(X_train_resampled, Y_train_resampled)

# 输出最佳参数
print(f"最佳参数: {grid_search.best_params_}")
print(f"最佳得分: {grid_search.best_score_}")

# 使用最佳参数训练最终模型
best_model = grid_search.best_estimator_

最优参数如图：

附：实验结果记录

文件夹中有网站的分数截图，下表是对这些分数的具体说明

模型	分数
LR	0.383851
LR+param grid	0.382004
LR+param_grid+class_weighted	0.506784
随机森林	0.338977
svm	0.333333
XGBoost	0.372797
XGBoost+param_grid	0.36659
集成学习LR+RF+XGBoost	0.384489

XGBoost:

最佳参数: {‘subsample’: 0.9, ‘n_estimators’: 200, ‘max_depth’: 7, ‘learning_rate’: 0.1, ‘colsample_bytree’: 0.8}
最佳得分: 0.7601263601263601

LR:

最佳参数: {‘C’: 1, ‘max_iter’: 100, ‘solver’: ‘lbfgs’}
最佳得分: 0.5195390195390195